Закон збереження імпульсу
Замкнені системи тіл
У фізиці тіла, що взаємодіють між собою, називають системою тіл. Ті сили, з якими взаємодіють тіла системи, називаються внутрішніми силами, а сили, з якими тіла системи взаємодіють з іншими тілами, що не входять до системи, називають зовнішніми силами.
Наприклад, більярдний стіл та кульки на ньому можна розглядати, як систему тіл (Мал. 1).
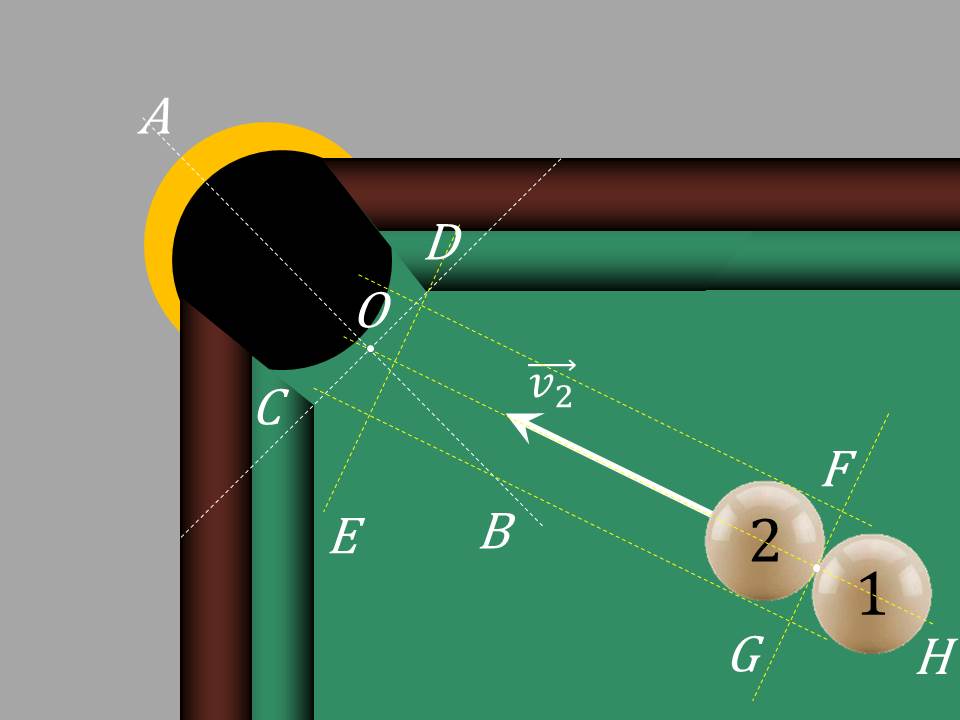
Сили, з якими взаємодіють кулі між собою — внутрішні; сили, з якими взаємодіють кулі зі столом теж внутрішні; сила тяжіння, що діє і на кожну кулю, і на стіл — зовнішня.
В розглянутому випадку, як і у багатьох інших, силу опору повітря можна не враховувати тому, що вона дуже незначна порівняно із іншими силами.
- Замкнені системи тіл —
- це такі системи, у яких зовнішні сили, які діють на систему зрівноважені або значно менші від внутрішніх сил системи.
Таким чином, ми можемо вважати нашу систему стіл-кульки замкненою.
Закон збереження імпульсу
Формулювання та формула закону
Ми знаємо, що, у результаті взаємодії, змінюється швидкість тіл. Отже, змінюються і їхні імпульси. Цю зміну в замкнених системах тіл описує закон збереження імпульсу.
- Закон збереження імпульсу
- У замкненій системі тіл векторна сума імпульсів тіл до взаємодії дорівнює векторній сумі імпульсів тіл після взаємодії.
Формулою цей закон записується так: \[\vec{p}_{01}+\vec{p}_{02}+\ldots+\vec{p}_{0n}=\vec{p}_{1}+\vec{p}_{2}+\ldots+\vec{p}_{n}\]
Тут \(\vec{p}_{01}\), \(\vec{p}_{02}\), \(\vec{p}_{0n}\) — імпульси тіл системи до взаємодії, а \(\vec{p}_{1}\), \(\vec{p}_{2}\), \(\vec{p}_{n}\) — імпульси тіл системи після взаємодії.
При розв'язуванні задач замість \(\vec{p}_n\) зручно записувати \(m\vec{v}_n\), де \(n\) — порядковий номер тіла, та супроводжувати розв'язування малюнком. Побачимо це трохи згодом.
Приклади прояву закону
До прикладів дії закону збереження імпульсу належать такі явища, як рух кульок більярду після зіткнення, віддача вогнепальної зброї, реактивний рух тощо.
Окремі приклади задач
Пружний удар
Пружним ударом називають таку взаємодію (зіткнення), яка супроводжується пружною деформацією тіл. Після такого удару тіла системи не зв'язані одне з одним.
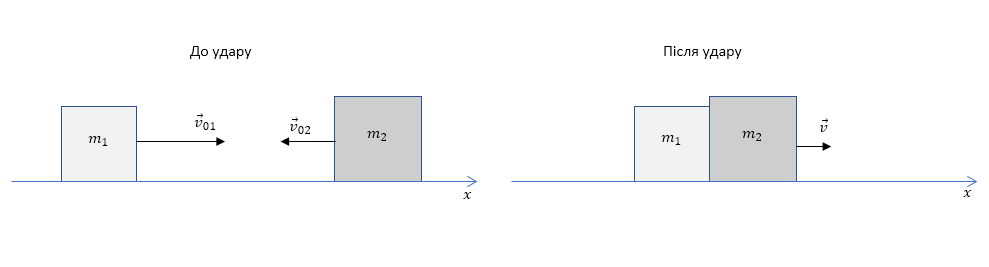
На Мал.1 показано швидкості тіл до взаємодії пружним ударом, а на малюнку Мал.2 - після взаємодії.
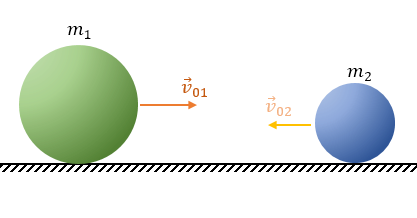

Для такої взаємодії, як на малюнку, закон збереження імпульсу запишеться так: \[m_1\vec{v}_{01}+m_2\vec{v}_{02}=m_1\vec{v}_{1}+m_2\vec{v}_2\]
Приклад 1
Задача
Дві кульки масами \(2\,\text{кг}\) та \(1{,}5\,\text{кг}\) рухаються назустріч одна одній. Швидкість важчої кульки \(1\,\frac{\text{м}}{\text{с}}\), а легшої — \(2\,\frac{\text{м}}{\text{с}}\). Після зіткнення кульки рухаються у протилежних напрямах. Якою стала швидкість важчої кульки після удару, якщо легша котиться зі швидкістю \(1\,\frac{\text{м}}{\text{с}}\)?
Розв'язання:
Виконаємо малюнок до задачі:
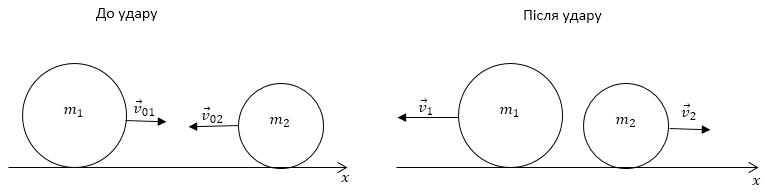
| Дано: | Розв'язання: |
|
\(m_1=2\,\text{кг}\) \(v_{2}=1\,\frac{\text{м}}{\text{с}}\) |
Сума імпульсів тіл до взаємодії: \(m_1v_{01}-m_2v_{02}\); Після взаємодії: \(-m_1v_1+m_2v_2\). За законом збереження імпульсу \(m_1v_{01}-m_2v_{02}=\) \(=m_2v_2-m_1v_1\), звідки
\(m_1v_1=m_2v_2-m_1v_{01}+m_2v_{02}\), |
| \(v_1-?\) |
Непружний удар
Непружним ударом називають таку взаємодію (зіткнення), яка супроводжується пластичною деформацією тіл. Після такого удару тіла системи рухаються, як одне ціле. На Мал.2 показано тіла до непружного удару, а на Мал.4 — після пружного удару.
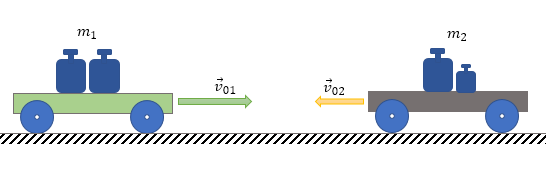
Для зображеної на малюнку взаємодії закон збереження імпульсу матиме вигляд: \[m_1\vec{v}_{01}+m_2\vec{v}_{02}=\left(m_1+m_2\right)\vec{v}\]
Приклад 2
Задача
Два тіла масами \(30\) та \(50\,\text{кг}\) рухаються назустріч одне одному. Швидкість першого тіла \(2\,\text{м/с}\), швидкість другого \(1\,\text{м/с}\). Якої швидкості набудуть ці тіла після непружного удару?
Розв'язання:
Виконаємо малюнок до задачі:
| Дано: | Розв'язання: |
|
\(m_1=30\,\text{кг}\) |
Сума імпульсів тіл до взаємодії: \(m_1v_{01}-m_2v_{02}\); Після взаємодії: \((m_1+m_2)v\). За законом збереження імпульсу \(m_1v_{01}-m_2v_{02}=(m_1+m_2)v\) звідки
\(v=\frac{m_1v_{01}-m_2v_{02}}{m_1+m_2}\), |
| \(v-?\) |
Приклад 3
Задача
Куля масою \(9\text{г}\) ,яка летіла зі швидкістю \(200\text{м/с}\) ,вдарилася в нерухомий дерев'яний брусок масою \(500\text{г}\) та застрягла у ньому. Визначити швидкість бруска після взаємодії
Розв'язання:
Виконаємо малюнок до задачі:

| Дано: | Розв'язання: |
|
\(m_1=0{,}009\,\text{кг}\) |
Сума імпульсів тіл до взаємодії: \(m_1v_{01}+m_2v_{02}\); Після взаємодії: \((m_1+m_2)v\). За законом збереження імпульсу \(m_1v_{01}+m_2v_{02}=(m_1+m_2)v\) звідки
\(v=\frac{m_1v_{01}-m_2v_{02}}{m_1+m_2}\), |
| \(v-?\) |
