Ділення десяткового дробу на натуральне число
Давай розглянемо таку ситуацію: \(\color{#1E90FF}{9{,}2}\textit{ кг}\) цукру потрібно розфасувати у п'ять однакових пакетів. Як це зробити?
Звичайно, ти знаєш, що \(9{,}2 \textit{ кг}=9200\textit{ г}\) і виконати цю дію дуже просто: \(9200\textit{ г}:5=1840\textit{ г}=1{,}84\textit{ кг}\).
Розв'язком цієї задачі є дія \(\color{#1E90FF}{9{,}2}:\color{green}{5}=\color{#6872C4}{1{,}84}\).
Як виконувати такі дії з дробами? Давай це з'ясуємо. Будемо виконувати цю дію в стовпчик. Спершу беремо по \(\color{#6872C4}{1}\):
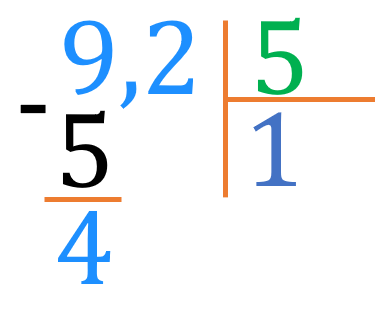
Отримали в остачі \(\color{#1E90FF}{4}\). Маємо зносити наступну цифру \(\color{#1E90FF}{2}\). Але перед нею стоїть кома! Кому маємо записати до частки перед тим, як зносити цифру за нею, а далі виконуємо ділення звичним чином.
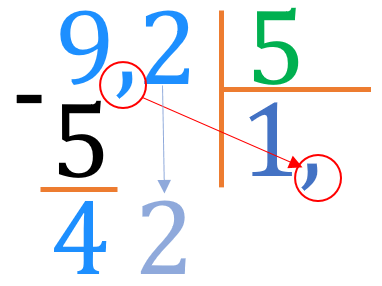
Отже, запам'ятаємо:
Продовжуємо виконувати ділення. \(\color{#1E90FF}{42}\) ділимо на \(\color{green}{5}\). Беремо по \(\color{#6872C4}{8}\).
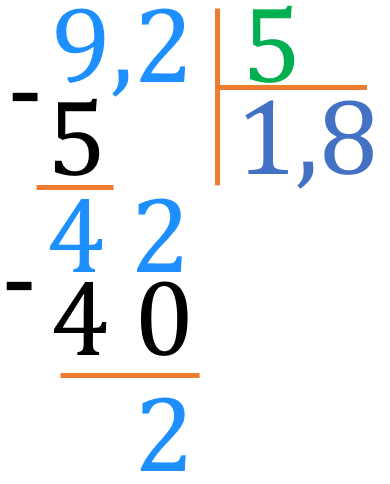
Отримали в остачі \(\color{#1E90FF}{2}\). Що далі? А далі — час згадати, що до числа \(\color{#1E90FF}{9{,}2}\) можна дописати у кінці нуль, і при цьому число не зміниться: \(\color{#1E90FF}{9{,}2}=\color{#1E90FF}{9{,}20}\). Тому до остачі \(\color{#1E90FF}{2}\) можемо дописати нуля:
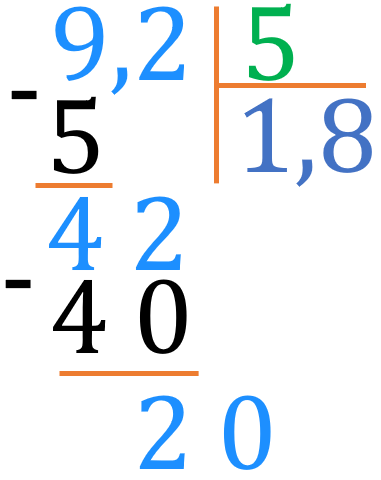
Завершуємо дію:
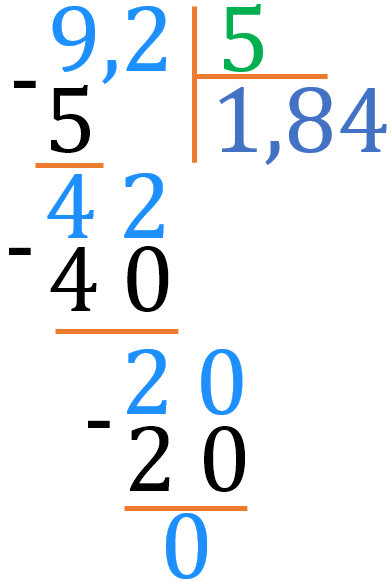
Отже, отримали те саме: \(\color{#1E90FF}{9{,}2}:\color{green}{5}=\color{#6872C4}{1{,}84}\). Таким чином, ми з'ясували, що ділення десяткового дробу на натуральне число можна виконувати в стовпчик.
Ділення десяткового дробу на натуральне число в стовпчик виконується майже так, як ділення натуральних чисел. Відміна лише в тому, що в частці треба на певному місці поставити кому і можна дописати нулі справа у дробовій частині.
Розглянемо ще декілька прикладів:
Приклад 1
Виконати ділення \(1{,}2:5\).
Розв'язання:
У даному прикладі в діленому \(\color{#1E90FF}{1{,}2}\) є тільки одна ціла, а дільник — п'ять. Оскільки \(\color{#1E90FF}{1}\) менше за \(\color{green}5\), у частку доразу пишемо \(\color{#1E90FF}{0}\) і ставимо кому. Тоді ділимо не звертаючи уваги на кому (доразу на \(\color{#1E90FF}{12}\)).
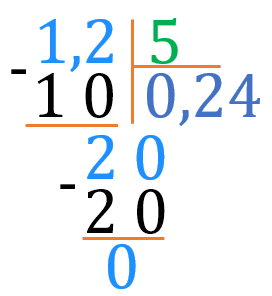
Приклади, подібні до розглянутого, легко розв'язувати, якщо мати на увазі наступне:
Якщо ціла частина дробу менша за ділене, то у частку одразу пишемо нуль, ставимо кому і зносимо по одній цифрі після коми.
Подивись, як цим користуватися на іще одному прикладі:
Приклад 2
Виконати ділення \(0{,}1:2\).
Розв'язання:
У даному прикладі в діленому нуль цілих. Доразу записуємо \(0\) і ставимо кому до частки. Зносимо цифру після коми \(\color{#1E90FF}{1}\). Але \(1\) на \(2\) не ділиться! Маємо дописати нуля. Оскільки це вже друга цифра, яку зносимо, підряд, то в частку теж пишемо \(0\). Далі ділимо отриманих \(10\) на \(2\) і отримуємо у результаті \(0{,}05\).
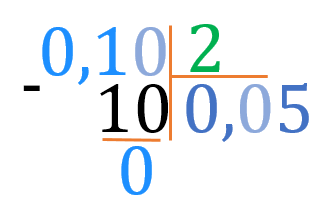
Розв'яжи самостійно
Завдання 1.
Виконай ділення: \(3{,}2:8\)
Завдання 2.
Виконай ділення: \(0{,}48:6\)
Завдання 3.
Виконай ділення: \(53{,}4:15\)

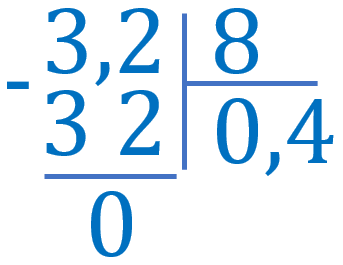
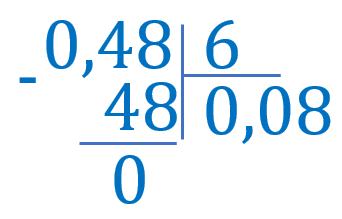
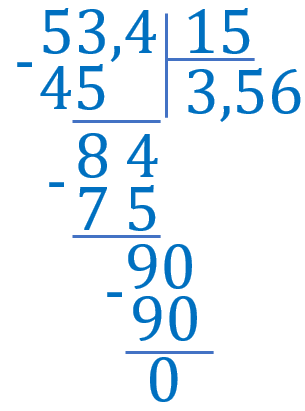
Перед тим, як зносити цифру після коми до остачі, зносимо кому до частки.