Імпульс тіла. Імпульс сили
Імпульс тіла
Означення імпульсу
Із повсякденного життя нам знайоме слово "імпульс". У біології говорять про нервовий імпульс, про підлітків часто кажуть, що вони мають імпульсивний характер. У фізиці імпульс — це фізична величина. В цьому розділі ми познайомимося з імпульсом тіла та імпульсом сили.
- Імпульс тіла —
- це векторна фізична величина, яка дорівнює добутку маси тіла на швидкість його руху.
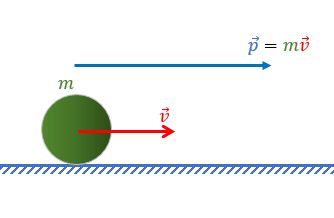
Імпульс тіла позначають \(\vec{p}\). Якщо маса тіла \(m\) і його швидкість \(\vec{v}\), то формула обчислення імпульсу: \[\vec{p}=m\vec{v}\]
Одиниця вимірювання імпульсу тіла — кілограм-метр за секунду: \[\left[p\right]=1\frac{\text{кг}\cdot\text{м}}{\text{с}}\]
Напрям вектора імпульсу завжди збігається з напрямом вектора швидкості (Мал. 1)
Logoptimus.net
Розв'язуємо задачі
Перед тим, як іти далі, розглянемо задачі:
Приклад 1
Задача
Знайти імпульс пішохода масою \(60\,\text{кг}\), який рухається
зі швидкістю \(1{,}5\,\frac{\text{м}}{\text{с}}\).
| Дано: | Розв'язання: |
|
\(m=60\,\text{кг}\) \(v=1{,}5\,\frac{\text{м}}{\text{с}}\) |
\(p=mv\); \(p=60\,\text{кг}\cdot 1{,}5\,\frac{\text{м}}{\text{с}}=\) \(=90\,\frac{\text{кг}\cdot\text{м}}{\text{с}}\). Відповідь: \(90\,\frac{\text{кг}\cdot\text{м}}{\text{с}}\). |
| \(p-?\) |
Приклад 2
Задача
Знайти імпульс вінтажного автомобіля масою \(10\,\text{т}\), який
рухається з швидкістю \(36\,\frac{\text{км}}{\text{год}}\), і
легкового автомобіля масою \(1\,\text{т}\), що рухається з
швидкістю \(25\,\frac{\text{м}}{\text{с}}\).
| Дано: | Розв'язання: |
|
\(m_1=10000\,\text{кг}\) \(v_1=10\,\frac{\text{м}}{\text{с}}\) \(m_2=1000\,\text{кг}\) \(v_2=25\,\frac{\text{м}}{\text{с}}\) |
\(p=mv\); \(p_1=10000\,\text{кг}\cdot 10\,\frac{\text{м}}{\text{с}}=\) \(=100000\,\frac{\text{кг}\cdot\text{м}}{\text{с}}\). \(p_2=1000\,\text{кг}\cdot 25\,\frac{\text{м}}{\text{с}}=\) \(=25000\,\frac{\text{кг}\cdot\text{м}}{\text{с}}\). Відповідь: \(10^5\,\frac{\text{кг}\cdot\text{м}}{\text{с}}\); \(2{,}5\cdot 10^4\,\frac{\text{кг}\cdot\text{м}}{\text{с}}\). |
|
\(p_1-?\) \(p_2-?\) |
Приклад 3
Задача
З якою швидкістю має летіти хокейна шайба масою
\(160\,\text{г}\), щоб її імпульс дорівнював імпульсові кулі
масою \(8\,\text{г}\), яка летить зі швидкістю
\(600\,\frac{\text{м}}{\text{с}}\)?.
| Дано: | Розв'язання: |
|
\(m_1=0{,}16\,\text{кг}\) \(m_2=0{,}008\,\text{кг}\) \(v_2=600\,\frac{\text{м}}{\text{с}}\) \(p_1=p_2\) |
\(p=mv\); \(p_1=p_2\); \(m_1v_1=m_2v_2\); \(v_1=\frac{m_2v_2}{m_1}\) \(v_1=\frac{0{,}008\,\text{кг}\cdot 600\,\frac{\text{м}}{\text{с}}}{0{,}16\,\text{кг}}=30\,\frac{\text{м}}{\text{с}}\). Відповідь: \(30\,\frac{\text{м}}{\text{с}}\). |
| \(v_1-?\) |
Спробуйте самостійно розв'яжіть у зошиті задачі із завдання. Для самоперевірки натисніть кнопку "Показати відповідь"
Задача 1.
Визначити імпульс футбольного м'яча масою \(400\,\text{г}\), якому надали швидкості \(25\,\frac{\text{м}}{\text{с}}\).
Задача 2.
Яка маса візка, що рухаючись зі швидкістю \(2\,\frac{\text{м}}{\text{с}}\), має імпульс \(24\,\frac{\text{кг}\cdot\text{м}}{\text{с}}\)?
Кількість руху. Фізичний зміст імпульсу
Імпульс тіла часто називають просто імпульсом, або кількістю руху.
Чому імпульс тіла має другу назву "кількість руху"? Це стає зрозумілим, якщо розглянути фізичний зміст цієї величини
Щоб краще зрозуміти останнє твердження, розглянемо ще одну величину — імпульс сили.
Імпульс сили
Означення імпульсу сили
Почнемо одразу з означення цієї фізичної величини.
- Імпульс сили —
- це векторна фізична величина, яка дорівнює добутку сили на час її дії на тіло.
Імпульс сили записують так: \[\vec{F} t\] де \(\vec{F}\) — сила, \(t\) — час її дії.
Одиниця вимірювання імпульсу сили — ньютон-секунда: \[\left[Ft\right]=1\,\text{Н}\cdot\text{с}\]
Давайте нагадаємо другий закон Ньютона, записаний у такій формі: \(\vec{F}=m\vec{a}\).
Прискорення, у свою чергу, запишемо \(\vec{a}=\frac{\vec{v}-\vec{v_0}}{t}\) і підставимо до попередньої формули: \[\vec{F}=m\frac{\vec{v}-\vec{v_0}}{t}\].
Помножимо обидві частини отриманого рівняння на час \(t\): \[\vec{F}t=\frac{m(\vec{v}-\vec{v_0})}{t}t\]
Після скорочення на \(t\) і розкриття дужок у правій частині рівняння отримуємо \[\vec{F}t=m\vec{v}-m\vec{v_0}\]
Розглянемо цю формулу детальніше. У її лівій частині знаходиться імпульс сили, а у правій — зміна імпульсу тіла. Таким чином
Імпульс сили дорівнює зміні імпульсу тіла
Ця формула пов'язує силу, що діє на тіло, та імпульс цього тіла. Часто, при розв'язуванні задач, доводиться мати справу не лише з імпульсом тіла \(\vec{p}\), а зі зміною імпульсу \(\Delta \vec{p}\). Ця зміна може відбутися тільки під дією якоїсь сили, і має пройти якійсь час. \[\Delta \vec{p}=m\vec{v}-m\vec{v_0}\] Якщо під час руху маса тіла не змінюється, то \(\Delta \vec{p}=m\left(\vec{v}-\vec{v_0}\right)\).
У випадку, коли початкова швидкість дорівнює нулю, маємо: \[\vec{F}t=m\vec{v}\,~~(\textit{при}\,v_0=0)\]
Останній вираз і пояснює фізичний зміст імпульсу тіла, розглянутий вище.
В загальному випадку, завжди \(\vec{F}t=\Delta \vec{p}\).
Розв'язуємо задачі
Приклад 4
Задача
Поїзд, маса якого \(2000\text{т}\), рухаючись прямолінійно,
збільшив швидкість від \(36\) до
\(72\frac{\text{км}}{\text{год}}\). Визначити зміну імпульсу.
| Дано: | Розв'язання: |
|
\(m=2\cdot 10^6\,\text{кг}\) \(v_0=10\,\frac{\text{м}}{\text{с}}\) \(v=20\,\frac{\text{м}}{\text{с}}\) |
\(\Delta p=mv-mv_0\); Маса залишається незмінною, тому \(\Delta p=m(v-v_0)\); \(\Delta p=2\cdot10^6\,\text{кг}\left(20\,\frac{\text{м}}{\text{с}}-10\,\frac{\text{м}}{\text{с}}\right)=\) \(=2\cdot10^7\,\frac{\text{кг}\cdot\text{м}}{\text{с}}\). Відповідь: \(2\cdot10^7\,\frac{\text{кг}\cdot\text{м}}{\text{с}}\). |
| \(\Delta p-?\) |
Приклад 5
Задача
Рух матеріальної точки описується рівнянням \(x=5-8t+4t^2\).
Вважаючи, що маса точки дорівнює \(2\,\text{кг}\), визначити
імпульс через \(2\,\text{с}\) і через \(4\,\text{с}\) після
початку відліку часу, а також силу, що викликала цю зміну
імпульсу.
| Дано: | Розв'язання: |
|
\(x=5-8t+4t^2\) \(m=2\,\text{кг}\) \(t_1=2\,\text{с}\) \(t_2=4\,\text{с}\) |
Із рівняння руху \(x=x_0+v_0t+\frac{at^2}{2}\) знаходимо: \(v_0=-8\,\frac{\text{м}}{\text{с}};\;\) \(a=8\,\frac{\text{м}}{\text{с}^2}\) \(p_1=mv_1,\;\) \(p_2=mv_2\). Швидкість рівноприскореного руху \(v_1=v_0+at_1,\;v_2=v_0+at_2\). \(v_1=-8\,\frac{\text{м}}{\text{с}}+8\,\frac{\text{м}}{\text{с}^2}\cdot2\,\text{с}=8\,\frac{\text{м}}{\text{с}}\). \(v_2=-8\,\frac{\text{м}}{\text{с}}+8\,\frac{\text{м}}{\text{с}^2}\cdot4\,\text{с}=24\,\frac{\text{м}}{\text{с}}\). Шукані імпульси \(p_1=2\,\text{кг}\cdot8\,\frac{\text{м}}{\text{с}}=16\,\frac{\text{кг}\cdot\text{м}}{\text{с}}\) \(p_2=2\,\text{кг}\cdot24\,\frac{\text{м}}{\text{с}}=48\,\frac{\text{кг}\cdot\text{м}}{\text{с}}\) |
|
\(p_1-?\) \(p_2-?\) \(F-?\) |
|
|
Силу знайдемо із рівняння \(Ft=\Delta p \Rightarrow
F=\frac{\Delta p}{t}\), де \(t=t_2-t_1\) і \(\Delta
p=p_2-p_1\): \[F=\frac{p_2-p_1}{t_2-t_1}\] \[F=\frac{(48-16)\,\frac{\text{кг}\cdot\text{м}}{\text{с}}}{(4-2)\,\text{с}}=16\,\text{Н}\] Відповідь: \(16\,\frac{\text{кг}\cdot\text{м}}{\text{с}};~48\,\frac{\text{кг}\cdot\text{м}}{\text{с}};~16\,\text{Н}\). |
|
Задача 3.
Знайдіть імпульс сили, якщо внаслідок її дії на тіло масою \(5\,\text{кг}\) швидкість тіла змінилася з \(5\,\frac{\text{м}}{\text{с}}\) до \(20\,\frac{\text{м}}{\text{с}}\).
Задача 4.
За який час сила \(20\,\text{Н}\) змінить швидкість візка масою \(2\,\text{кг}\) з \(5\,\frac{\text{м}}{\text{с}}\) до \(10\,\frac{\text{м}}{\text{с}}\)?

Фізичний зміст імпульсу
Імпульс тіла є мірою сили, яку необхідно прикласти до даного тіла, що перебуває у стані спокою, щоб надати йому даної швидкості за деякий час