Ділення десяткового дробу на десятковий дріб
Що ми вже вміємо
Привіт! Для того, щоб гарно навчитися ділити на десятковий дріб, давай нагадаємо ті знання, що у нас уже є. А саме:
- Як поділити десятковий дріб на натуральне число
- Одну із властивостей ділення
Для цього виконаємо декілька завдань. Почнемо із ділення десяткового дробу на натуральне число.
Завдання 1.
Виконай ділення: \(3{,}6:8\)
Завдання 2.
Виконай ділення: \(12{,}5:5\)
Тепер розглянемо завдання, які допоможуть нам згадати одну властивість ділення. Цю властивість ми будемо дуже активно використовувати при діленні будь-яких чисел на десятковий дріб.
Завдання 3.
Знайди частку: \(\color{#556B2F}{12}:\color{#6872C4}{6}\)
Завдання 4.
Виконай ділення: \(\color{#556B2F}{12}\color{#1E90FF}{0}:\color{#6872C4}{6}\color{#1E90FF}{0}\)
Завдання 5.
Виконай ділення: \(\color{#556B2F}{12}\color{#1E90FF}{00}:\color{#6872C4}{6}\color{#1E90FF}{00}\)
Давай придивимось до завдань 3, 4 і 5. У кожному із них частка дорівнює \(2\). При чому, у завданні 4 ділене \(\color{#556B2F}{12}\color{#1E90FF}{0}\) і дільник \(\color{#6872C4}{6}\color{#1E90FF}{0}\) одночасно у десять разів більші за ділене і дільник у завданні 3. А у завданні 5 — у сто разів. Це і відображує ту властивість ділення, про яку йшла мова:
Саме цю властивість ми використаємо, щоб ділити будь-яке число на десятковий дріб.
Як ділити десятковий дріб на десятковий дріб
Нехай перед нами стоїть завдання знайти частку чисел \(\color{#4682B4}{12{,}63}\) і \(\color{#6B8E23}{0{,}3}\). Виразом ця частка записується як \[\color{#4682B4}{12{,}63}:\color{#6B8E23}{0{,}3}.\] Ділене \(\color{#6B8E23}{0{,}3}\) є десятковим дробом. Але якщо його збільшити у 10 разів, отримаємо натуральне число \(\color{#6B8E23}{3}\)! Ділити на натуральне число ми вже вміємо. От і настав час скористатися властивістю, яку щойно повторили: нам потрібно у цьому прикладі збільшити одночасно ділене і дільник у \(10\) разів. Отримаємо такий приклад: \[\color{#4682B4}{126{,}3}:\color{#6B8E23}{3}.\] Сподіваюся, для тебе не проблема знайти його значення \(\color{#4682B4}{126{,}3}:\color{#6B8E23}{3}=\color{#FF6347}{42{,}1}\). А отже і \(\color{#4682B4}{12{,}63}:\color{#6B8E23}{0{,}3}=\color{#FF6347}{42{,}1}\).
Таким чином, можемо вказати загальне правило ділення будь-якого числа на десятковий дріб:
Щоб поділити десятковий дріб на десятковий дріб, треба:
- перенести коми в діленому і в дільнику вправо на стільки цифр, скільки їх міститься після коми у дільнику;
- виконати ділення на натуральне число.
Розглянемо, як користуватися цим правилом.
Приклад 1
Знайдіть частку \(3{,}2:0{,}4\).
Розв'язання:
У даному виразі дільник \(0{,}4\) має одну цифру після коми. Тому в діленому та у дільнику переносимо коми на одну цифру:
\[3{,}2:0{,}4=32:4=8\]
Відповідь: 8.
Приклад 2
Знайдіть частку \(0{,}36:0{,}9\).
Розв'язання:
У даному виразі дільник \(0{,}9\) має одну цифру після коми. Тому в діленому та у дільнику переносимо коми на одну цифру:
\[0{,}36:0{,}9=3{,}6:9\]
Виконавши ділення на натуральне число, отримуємо \(0{,}4\).
Відповідь: \(0{,}4\).
Приклад 3
Знайдіть частку \(19{,}798:5{,}21\).
Розв'язання:
У даному виразі дільник \(5{,}21\) має дві цифри після коми. Тому в діленому та у дільнику переносимо коми на дві цифри:
\[19{,}798:5{,}21=1979{,}8:521\]
Виконавши ділення на натуральне число в стовпчик, отримуємо \(3{,}8\).
Відповідь: \(3{,}8\).
Розв'яжи приклади із завдань 6-8 самостійно. Щоб перевірити правильність, натисни кнопку "Показати відповідь".
Завдання 6.
Знайди частку: \(3{,}5:0{,}7\)
Завдання 7.
Виконай ділення: \(0{,}56:0{,}8\)
Завдання 8.
Виконай ділення: \(0{,}026:0{,}65\)

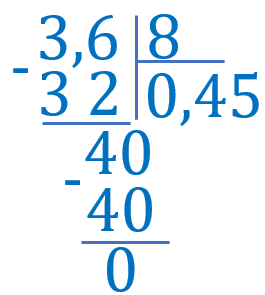
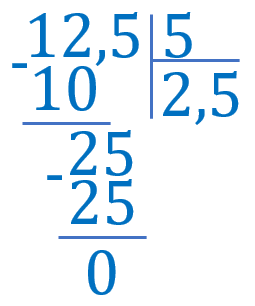
Якщо ділене і дільник збільшити одночасно в \(10\), \(100\), \(1000\) і т.д. разів, то частка не зміниться