7. Квадратична функція та її графік
7.1 Означення квадратичної функції
- Квадратичною функцією
- називають функцію, яку можна задати у вигляді \(y=ax^2+bx+c\),
де \(a, b, c\) — дійсні числа, при чому \(a\ne0\).
Свою назву ця функція отримала тому, що її аргумент знаходиться у другому степені (в квадраті). Подивимось на деякі із них: \(y=3x^2-2,~ y=-0{,}2x^2,~ y=3-2x+\frac{2x^2}{3}\) — все це приклади квадратичних функцій.
Давайте покажу, що я маю на увазі, на конкретному прикладі.
Приклад.
Записати функцію \(y=3-2x+\frac{2x^2}{3}\) у стандартному вигляді, та визначити значення \(a, b, c\).
Почнемо із того, що запишимо праву частину в стандартному вигляді (розмістимо члени в порядку спадання степеня змінної \(x\)):
\(y=\frac{2x^2}{3}-2x+3\).
І, нарешті, перепишимо у вигляді:
\(y=\frac{2}{3}x^2-2x+3\).
Тепер явно видно, що \(a=\frac{2}{3},~ b=-2,~c=3\).
Виконуючи подібні завдання, не треба забувати, що можливі випадки, коли \(b=0,~c=0\). У випадку, коли \(b=0,~ c=0,~ a=1\), отримуємо добре знайому нам функцію \(y=x^2\).
7.2 Графік квадратичної функції
Вигляд графіка
Графіком квадратичної функції є парабола. На Мал. 1 показано графіки декількох квадратичних функцій.
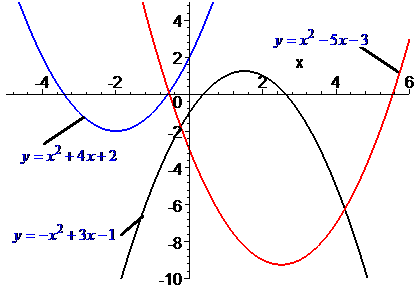
Мал. 1 - графіки квадратичних функцій.
Зображення з сайту http://yukhym.com
З малюнка видно, що вершини парабол знаходяться у різних точках. Крім того, вітки параболи, що є графіком функції \(y=-x^2+3x-1\) (показано чорним), напрямлені вниз, а решти — вгору. А ще важливими є точки, у яких графік функції перетинає координатні осі.
Маємо навчитися визначати всі ці речі. Почнемо.
Напрям віток параболи
Напрям віток графіка функції \(y=ax^2+bx+c\) визначається за значенням коефіцієнта \(a\). Вітки параболи напрямлені вгору, якщо \(a>0\), і вниз, коли \(a<0\).
Напрям віток параболи визначаємо за коефіцієнтом \(a\):
- якщо \(a>0\) — вітки напрямлені вгору;
- якщо \(a<0\) — вітки напрямлені вниз.
Координати вершини параболи
Щоб побудувати графік квадратичної функції, потрібно уміти визначати координати точки, в якій знаходиться вершина параболи, що є цим графіком.
Нехай вершина даної параболи знаходиться у точці з координатами \((m; n)\). Координату \(m\) визначають за формулою \[m=\frac{-b}{2a}\]. Координату \(n\) зручно шукати, підставивши знайдене число \(m\) у рівняння функції за значення аргументу, тобто \(n=am^2+bm+c\). Можна скористатися і формулою \[n=-\frac{b^2-4ac}{4a}\].
Координати \((m;n)\) вершини параболи знаходимо за формулами:
- \(m=\frac{-b}{2a}\);
- \(n=am^2+bm+c~~\) або \(~~n=-\frac{b^2-4ac}{4a}\).
Приклад.
Знайти координати вершини графіка функції \(y=3x^2-12x+1\).
Знайдемо координату \(x\) — число \(m\):
\(m=\frac{-b}{2a};~ m=\frac{-(-12)}{2\cdot3}=2\).
Знайдемо координату \(y\) — число \(n\):
Перший спосіб. Використаємо формулу \(n=am^2+bm+c\):
\(n=3\cdot2^2-12\cdot2+1=12-24+1=-11\).
Другий спосіб. Знайдемо \(n\) за формулою \(n=-\frac{b^2-4ac}{4a}\):
\(n=-\frac{(-12)^2-4\cdot3\cdot1}{4\cdot3}=-\frac{144-12}{12}=-11\).
Відповідь: \((2;-11)\)
Мушу зазначити, що на практиці не потрібно використовувати обидва способи, щоб знайти число \(n\). Оберіть собі один, зручніший для вас. Ним і користуйтеся.
Координати точок перетину параболи з осями координат
Точка перетину з віссю \(Oy\)
Точка перетину графіка квадратичної функції \(y=ax^2+bx+c\) з віссю ординат \(Oy\) має координати \((0; c\)).
Така точка для будь-якої квадратичної функції завжди лише одна.
Точки перетину з віссю \(Ox\)
Якщо графік функції \(y=ax^2+bx+c\) перетинає вісь абсцис, то точки перетину мають координати \((x_1; 0)\) і \((x_2; 0)\), де \(x_1,~ x_2\) – корені тричлена \(ax^2+bx+c\).
Графік квадратичної функції може не мати взагалі точок перетину з віссю \(Ox\), може мати дві такі точки, або тільки одну спільну точку з цією віссю. Розберемо кожний із випадків.
Парабола не перетинає вісь абсцис, коли виконується хоча б одна із умов:
- дискримінант квадратного тричлена \(ax^2+bx+c\), що задає функцію, — від'ємний (\(D<0\));
- вітки параболи напрямлені вгору (\(a>0\)) і ордината її вершини – додатна (\(n>0\));
- вітки параболи напрямлені вниз (\(a<0\)) і ордината її вершини – від'ємна (\(n<0\)).
Якщо парабола має з віссю \(Ox\) тільки одну спільну точку, то це означає, що вершина параболи знаходиться на осі абсцис.
Вершина параболи лежить на осі абсцис, коли:
- дискримінант квадратного тричлена \(ax^2+bx+c\), що задає функцію,дорівнює нулю (\(D=0\));
- ордината вершини параболи дорівнює нулю (\(n=0\)).
І, накінець, в усіх інших випадках парабола перетинає вісь \(Ox\) у двох точках. Найчастіше про це свідчить те, що дискримінант тричлена, що задає квадратичну функцію, – додатне число (\(D>0\)).
< Попередня тема Наступна тема >

Щоб успішно працювати з квадратичною функцією, треба: