8. Побудова графіка квадратичної функції

8.1 Кроки побудови графіка квадратичної функції

Для того, щоб побудувати графік функції \(y=ax^2+bx+c\), зручно скористатися послідовність кроків, представленою на схемі:

Користуючись даною схемою, можна побудувати ескіз графіка. Чим більше додаткових точок визначимо у останньому пункті, тим точніший ескіз отримаємо.

8.2 Приклади побудови графіків квадратичних функцій

Проілюструємо, як користуватися наведеною вище схемою для побудови графіка квадратичної функції.

Приклад 1. Побудувати графік функції \(y=x^2-2x-3\)

1. Визначимо напрямок віток параболи. У рівнянні даної функції \(a=1\), отже вітки її графіка напрямлені вгору.
2. Визначимо координати вершини параболи:
   \(m=\frac{2}{2\cdot1}=1\);  \(n=1^2-2\cdot1-3=-4\).
   Маємо, що вершина знаходиться у точці \((1;-4)\). Позначимо її на координатній площині, і проведемо пряму \(x=1\):

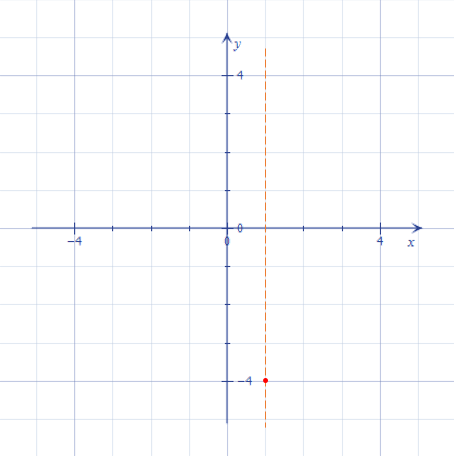
Мал. 1 - Вершина параболи знаходиться у точці \((1; -4)\), провели пряму \(x=1\)

3. Ордината перетину графіка з віссю \(Oy\) дорівнює вільному члену \(c\) рівняння функції. У нашому випадку \(c=-3\). Позначимо точку \((0;-3)\), і точку, симетричну їй відносно прямої \(x=m\), тобто \((2; -3)\):

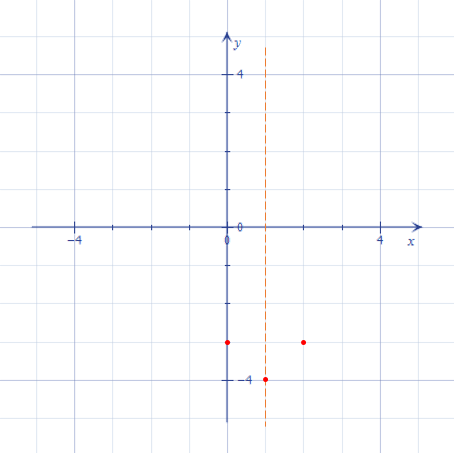
Мал. 2 - Точка перетину графіка з віссю \(Oy\), та симетрична їй відносно прямої\(x=1\)

4. Знайдемо абсциси точок перетину графіка з віссю \(Ox\) з умови \(ax^2+bx+c=0\):
   \(x^2-2x-3=0\). За теоремою, оберненою до теореми Вієта, маємо: \(x_1=-1,~x_2=3\).
   Отже, точки перетину параболи з віссю \(Ox\) мають координати \((-1; 0)\) і \((3; 0)\). Відкладемо їх:

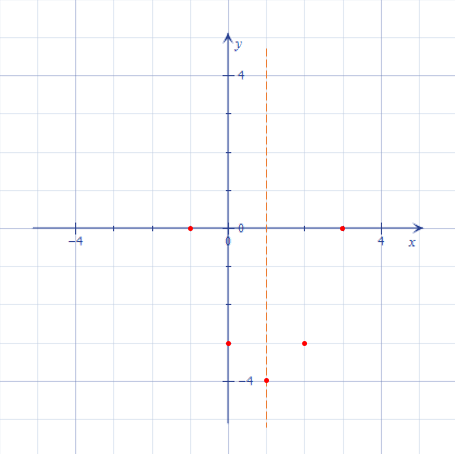
Мал. 3 - Тепер і точки перетину з віссю \(Ox\).

5. Візьмемо ще пару точок. Побудємо для цього таблицю значень:

   \(x\)	\(-2\)	\(4\)
   \(y\)	\(5\)	\(5\)

   і відкладемо точки із зазаначеними у таблиці координатами:

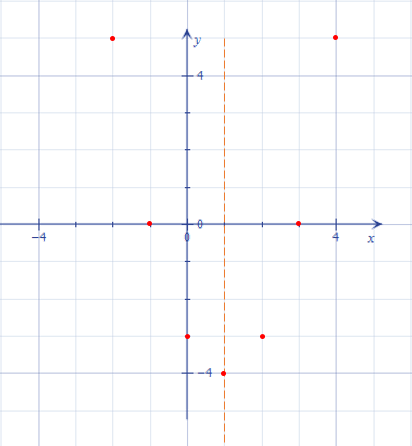
Мал. 4 - Ще більше точок!

6. І, на кінець, сполучаємо точки плавною лінією і не забуваємо підписати графік:

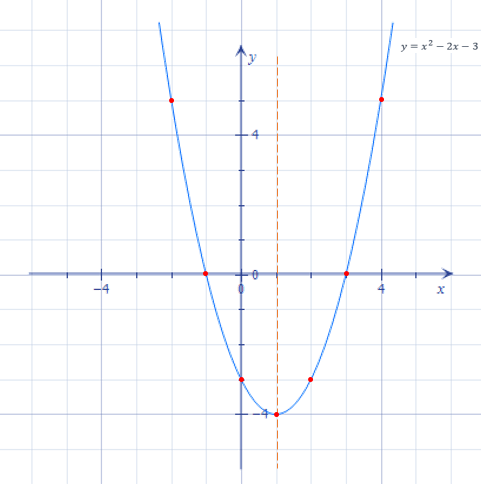
Мал. 4 - Графік функції \(y=x^2-2x-3\) у всій своїй красі.