1. Функція \(y=x^2\). Її графік та властивості
1.1 Функція \(y=x^2\) та її графік
Другий степінь числа дуже часто зустрічається при знаходженні різних величин. Найпростіший приклад такої величини – площа квадрата. Тому другий степінь числа ще називають його квадратом.

Якщо довжину сторони позначити \(a\), то площа квадрата буде дорівнювати \(a^2\) (\(S=a^2\)) . Для будь-якого значення \(a\) буде існувати єдине значення \(S\) .
Таким чином, можна стверджувати, що \(S\) є функцією від \(a\). Звичним для нас способом цю функцію можна записати так: \[y=x^2.\]
Побудуємо таблицю значень даної функції для іксів від \(-4\) до \(4\):
| \(x\) | \(-4\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) |
| \(y\) | \(16\) | \(9\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) | \(9\) | \(16\) |
Відкладемо отримані точки на координатній площині (Мал.2).
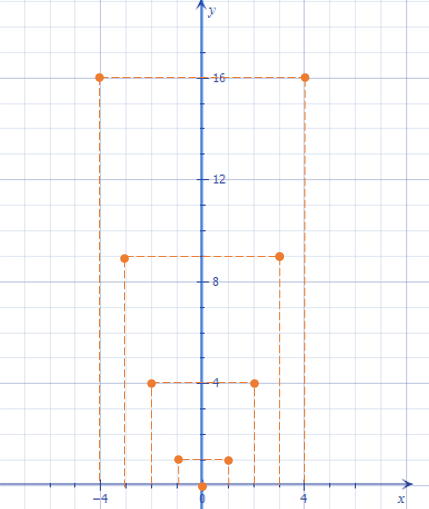
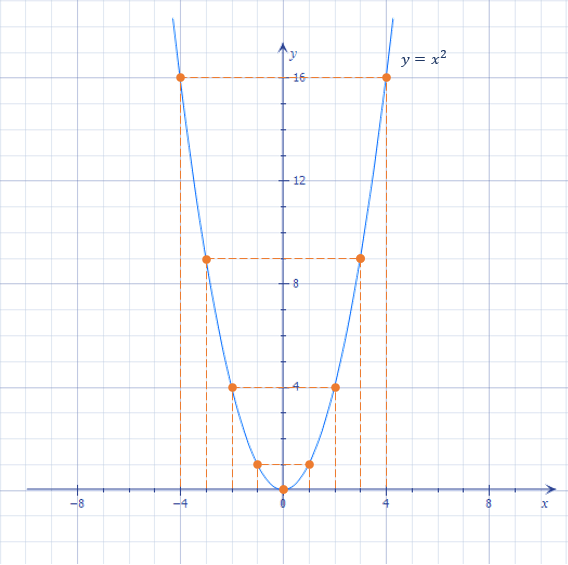
Сполучивши отримані точки плавною лінією, отримаємо графік функції (Мал.3). Така крива лінія називається параболою. Парабола складається із двох віток, які сходяться в точці, що називається вершиною параболи.
Отже,
З Mалюнка 3 видно, що графік функції \(y=x^2\) симетричний відносно осі ординат \(Oy\), а сама функція набуває найменшого значення, що дорівнює нулю, у точці \(x=0\). Найбільшого значення для даної функції не існує.
1.2 Властивості функції \(y=x^2\).
Розглянемо детальніше властивості функції \(y=x^2\):
- Область визначення функції – множина дійсних чисел
- Область значень функції – множина невід’ємних дійсних чисел
- Нуль функції — точка \(x=0\)
- Найменше значення функції — \(0\) в точці \(x=0\)
- Найбільшого значення функції не існує
- Функція спадає на проміжку \((-\infty; 0)\)
- Функція зростає на проміжку \((0; \infty)\)
- Функція парна, тобто \(y(x)=y(-x)\)

Графіком функції \(y=x^2\) є парабола, напрямлена вітками вгору, вершина якої знаходиться в початку координат точці \(O(0;0)\).