2. Арифметичний квадратний корінь

2.1 Що таке квадратний корінь

Щоб розібратися з квадратними коренями, давайте розглянемо просте рівняння \(x^2=9\).

Його розв’язками є числа \(x=-3\) і \(x=3\). Справді, підставивши їх у рівняння замість змінної , отримаємо правильні рівності \((-3)^2=9\) і \(3^2=9\).

Ці числа називаються квадратним коренем числа \(9\).

Квадратним коренем із числа \(a\)
 називається число, квадрат (другий степінь) якого дорівнює \(a\).

Сам процес знаходження значень квадратного кореня з якогось числа називають добуванням квадратного кореня із  числа.

Квадратним коренем з числа \(16\) є числа \(4\) і \(-4\), із числа \(25\) — числа \(5\) і \(-5\), із числа \(81\) — числа \(9\) і \(-9\). Як бачимо, квадратний корінь із додатного числа має два значення, однакових за модулем, але одне із  них додатне, а друге — від’ємне. Квадратний корінь із нуля має лише одне значення, і воно теж дорівнює нулю (бо тільки \(0^2=0\)).

А от із від’ємного числа квадратний корінь не має дійсного значення. Справді, якщо підносити до квадрату додатне число, отримаємо теж додатне число. Якщо підносити до квадрату від’ємне число — знову отримаємо додатне! (Ага, «мінус» на «мінус» дає «плюс»)!

Отже:

  • Квадратний корінь із додатного числа має два значення
  • Квадратний корінь з числа \(0\) дорівнює нулю
  • Квадратний корінь із від'ємного числа не добувається

 Квадратні корені зручно добувати, якщо добре знати квадрати чисел

Таблиця квадратів натуральних чисел від 1 до 99

Десятки Одиниці
0 1 2 3 4 5 6 7 8 9
1 100 121 144 169 196 225 256 289 324 361
2 400 441 484 529 576 625 676 729 784 841
3 900 961 1024 1089 1156 1225 1296 1369 1444 1521
4 1600 1681 1764 1849 1936 2025 2116 2209 2304 2401
5 2500 2601 2704 2809 2916 3025 3136 3249 3364 3481
6 3600 3721 3844 3969 4096 4225 4356 4489 4624 4761
7 4900 5041 5184 5329 5476 5625 5776 5929 6084 6241
8 6400 6561 6724 6889 7056 7225 7396 7569 7744 7921
9 8100 8281 8464 8649 8836 9025 9216 9409 9604 9801

 

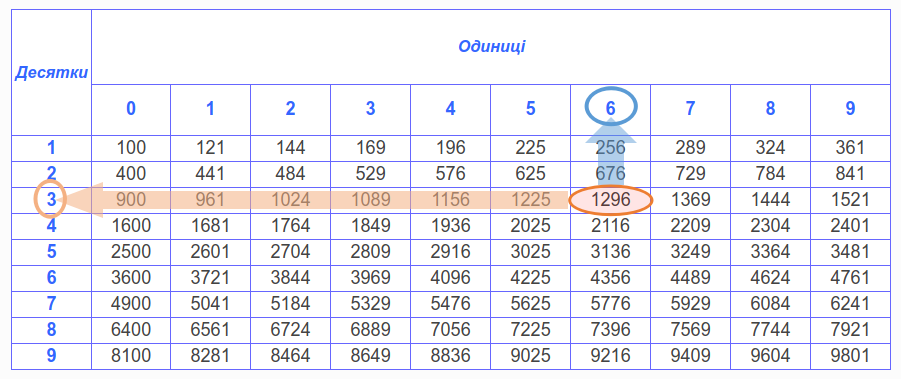
Подивимось, як користуватися цією таблицею для знаходження коренів.

Нехай нам потрібно знайти квадратний корінь із числа \(1296\). Для цього робимо такі кроки:

  1. Знаходимо число \(1296\) у таблиці
  2. У крайній лівій колонці навпроти нього— кількість десятків (\(3\))
  3. У верхньому рядку навпроти нього— кількість одиниць (\(6\))
  4. Пам'ятаючи про два значення квадратного кореня, отримуєм відповідь: \(36\) та \(-36\).

Logoptimus.net - Як знайти квадратний корінь

Мал. 1. - знаходимо корінь із \(1296\)
Завдання 1.

Користуючись таблицею квадратів, знайдіть значення квадратного кореня із \(\color{#008080}{1936}\)

\(44\) і \(-44\)

Завдання 2.

Користуючись таблицею квадратів, знайдіть значення квадратного кореня із \(\color{#008080}{5184}\)

\(72\) i \(-72\)

 

2.2 Арифметичний квадратний корінь

Щоб уникнути плутанини, пов’язаної із тим, що існує два значення кореня, у математиці ввели поняття арифметичного квадратного кореня.

Арифметичним квадратним коренем із числа \(a\)
 називається невід'ємне число, квадрат (другий степінь) якого дорівнює \(a\).

На практиці арифметичний квадратний корінь з числа  дуже часто називають просто коренем з числа .

Для позначення арифметичного квадратного кореня на письмі придумали спеціальний знак — радикал. Виглядає він ось так: square root of blank end root. Записувати число (чи вираз), з якого добуваємо корінь, потрібно під верхньою рискою радикала, слідкуючи за тим, щоб ця риска була такої самої довжини, як число або вираз під нею.

Наприклад, запишемо виразом «Корінь з виразу три ікс додати два дорівнює вісімнадцять»

Правильний запис: \(\sqrt{3x+2}=18\)

Неправильний запис: \(\sqrt{3x+}2=18\) (двійка не під знаком радикала)

Неправильний запис: \(\sqrt{3x+2=}18\) (знак рівності "заповз" під радикал).

Зрозуміло, що арифметичний квадратний корінь може мати тільки одне значення для будь-якого невід’ємного числа  \(\left(\sqrt{16}=4, \sqrt{81}=9, \sqrt{0}=0 \text{ і т.д.}\right){.}\)

Завдання 3.

Знайдіть значення виразу \(\color{#008080}{\sqrt{49}-\sqrt{25}}\)

\(\sqrt{49}-\sqrt{25}=7-5=2\)

Завдання 4.

Знайдіть значення виразу \(\color{#008080}{\sqrt{16+9}}\)

\(\sqrt{16+9}=\sqrt{25}=5\)

 

2.3 Рівняння \(x^2=a\)

Повернемось до рівняння \(x^2=9\), яке розглянули на початку. Ми побачили, що воно має два корені (\(-3 \text{ і } 3\)). Використовуючи означення арифметичного квадратного кореня, їх можна записати, як

 .\(x_1=-\sqrt{9} \text{ i } x_2=\sqrt{9}\).

Розглянуте рівняння є окремим випадком рівняння виду \(x^2=a\). Можемо записати, які розв’язки матиме це рівняння, в залежності від значення числа \(a\)

Рівняння \(x^2=a\)

  • при \(a>0\) має два корені
    • \(x_1=-\sqrt{a}\) і
    • \(x_2=\sqrt{a}\)
  • при \(a=0\) має один корінь
    • \(x=0\)
  • при \(a<0\) рівняння коренів не має.

Розв'язуванню таких рівнянь буде присвячено один із наступних уроків.

 

2.4 Як знайти квадратний корінь з числа

Знайти (добути) квадратний корінь із якогось числа
 означає знайти інше число, яке помножене саме на себе, дорівнює підкореневому числу.

Квадратні корені з цілих чисел

Пам'ятаємо, що:

\(\sqrt{0}=0\) і \(\sqrt{1}=1\)

Для того, щоб добути корінь із цілого числа, зручно користуватися таблицею квадратів, як ми розглянули вище. \(\sqrt{225}=15,~~\sqrt{81}=9\)  і т.д.

Але існують цілі числа, які не являються квадратом іншого цілого числа. Ну, наприклад, \(5\). Неможливо підібрати таке ціле число \(n\), щоб \(n^2=5\). В таких випадках можна використати спеціальні таблиці, або обчислювальну техніку (хоч би й калькулятор). Скориставшись останнім, визначимо, що \(\sqrt{5}\) — нескінченний десятковий дріб: \(\sqrt{5}=2{,}236067977...\).

 

Квадратні корені з круглих чисел

У багатьох випадках зручно обчислювати корені з круглих чисел. Це можна зробити усно, якщо число, утворене цифрами перед нулями є квадратом деякого числа, а решта нулів мають парну кількість. В цьому випадку добуваємо корінь з числа, утвореного цифрами перед нулями, і дописуємо вдвічі менше нулів, ніж у підкореневому числі.

Наприклад:

  1. Знайти \(\sqrt{400}\).

    Розв'язання: Перша четвірка є квадратом числа \(2\), а після неї нулів – два (парна кількість) \(\sqrt{\color{\green}{4}}=\color{Green}{2}\) і один нуль: \(\sqrt{\color{Green}{4}\underline{00}}=\color{OliveGreen}{2}\underline{0}\).
     

  2. Знайти \(\sqrt{2560000}\).

    Розв'язання: \(\sqrt{\color{Green}{256}\underline{0000}} =\color{Green}{16}\underline{00}\).
     

  3. Знайти \(\sqrt{121000000}\).

    Розв'язання: \(\sqrt{\color{Green}{121}\underline{000000}}=\color{Green}{11}\underline{000}\).
     

  4. Знайти \(\sqrt{\color{Green}{256}\underline{000}}\).

    Розв'язання: Кількість нулів непарна. Усно визначити неможливо. Результат — нескінченний десятковий дріб.
     

Квадратні корені зі звичайних дробів

Для того, щоб здобути арифметичний квадратний корінь із звичайного дробу, достатньо окремо обчислити корінь із чисельника та корінь із знаменника цього дробу.

Наприклад:

  1. Знайти \(\sqrt{\frac{64}{121}}\).

    \(\sqrt{\frac{\color{Green}{64}}{\color{Blue}{121}}}=\frac{\sqrt{\color{\green}{64}}}{\sqrt{\color{Blue}{121}}}=\frac{\color{Green}{8}}{\color{Blue}{11}}\)
     

  2. Обчислити \(\sqrt{\frac{3}{75}}\).

    Розв'язання: \(\sqrt{\frac{\color{Green}{3}}{\color{Blue}{75}}}=\sqrt{{\frac{\color{Green}{1}}{\color{Blue}{25}}}}=\frac{\sqrt{\color{Green}{1}}}{\sqrt{\color{Blue}{25}}}=\frac{\color{Green}{1}}{\color{Blue}{5}} \)

  3. Обчислити \(\sqrt\frac{25}{101}.\)

    Розв'язання: Арифметичний квадратний корінь з числа \(101\) - нескінченний десятковий дріб. Усно визначити неможливо.

Квадратні корені із десяткових дробів

Якщо підкореневе число — десятковий дріб із більше, ніж однією значущою цифрою після коми, то усно обчислити такий корінь можна тільки тоді, коли:

1)      із числа, що отримане з дробу шляхом відкидання десяткової коми та ведучих нулів, можна здобути корінь;

2)      кількість цифр після коми – парна.

Якщо дріб задовольняє наведеним умовам, то здобуваємо корінь з числа, отриманого в пункті 1) та відокремлюємо комою вдвічі менше цифр, ніж було після коми у підкореневому числі.

Наприклад:

  1. Обчислити \(\sqrt{0{,}0025}\).

    Розв'язання: Відкинувши десяткову кому з усіма нулями, отримаєм \(25\). З цього числа корінь усно добувається: \(\sqrt{25}=5\). У числі \(0{,}0025\) після коми чотири цифри — друга умова виконується теж. У результат записуємо \(5\), і відокремлюємо комою дві цифри, добавляючи нулі. Отримуємо \(0{,}05\).
    \(\sqrt{0{,}\underline{00\color{Blue}{25}}}=0{,}\underline{0\color{Blue}{5}}\).

  2. Обчислити \(\sqrt{6{,}25}\).

    Розв'язання: \(\sqrt{\color{Blue}{6}{,}\color{Blue}{\underline{25}}}=\color{Blue}{2}{,}\color{Blue}{\underline{5}}\).

  3. Обчислити \(\sqrt{62{,}5}\).

    Розв'язання: У підкореневому числі один знак після коми. Значення кореня — нескінченний дріб. Усно визначити неможливо.

 

2.5 Тотожність \(\left(\sqrt{a}\right)^2=a\)

Для будь-якого невід'ємного числа \(a\) виконується тотожність \(\left(\sqrt{a}\right)^2=a\). Дійсно, за означенням арифметичного квадратного кореня, якщо піднести цей корінь до другого степеня, отримаємо підкореневе число.

\(\left(\sqrt{4x}\right)^2=4x, \left(\sqrt{3x-2}\right)^2=3x-2\).

Дану тотожність зручно використовувати, коли потрібно позбутися квадратного кореня. Це може знадобитися, наприклад, при розв'язуванні рівнянь:

Приклад.

Розв'язати рівняння \(\sqrt{2x+2}=4\)

Розв'язання:

Піднесемо обидві частини рівняння до другого степеня:

\(\left(\sqrt{2x+2}\right)^2=4^2,\)

У лівій частині скористаємось тотожністю \(\left(\sqrt{a}\right)^2=a\), у правй маємо \(4^2=16\):

\(2x+2=16\),

Розв'яжемо отримане просте рівняння:

\(2x=14\),
\(x=7\).

Відповідь: \(7\).

Завдання 5.

Обчисліть: \(\color{#008080}{\left(\sqrt{4}\right)^2}\)

\(4\)

Завдання 6.

Обчисліть: \(\color{#008080}{-\left(\sqrt{9}\right)^2}\)

\(-9\)

Завдання 7.

Обчисліть: \(\color{#008080}{\left(4\sqrt{9}\right)^2}\)

\(\left(4\sqrt{9}\right)^2=4^2\cdot\left(\sqrt{9}\right)^2=16\cdot9=144\)

Наступного уроку ми навчимося розв'язувати інші вправи із арифметичним квадратним коренем.

Остання зміна: четвер, 14 січня 2021, 11:19