Прямокутний трикутник та його властивості
Елементи прямокутного трикутника
Давайте подивимось на прямокутний трикутник \(ABC\) із \(\angle C =90^\circ\), якого зображено на Мал.1:
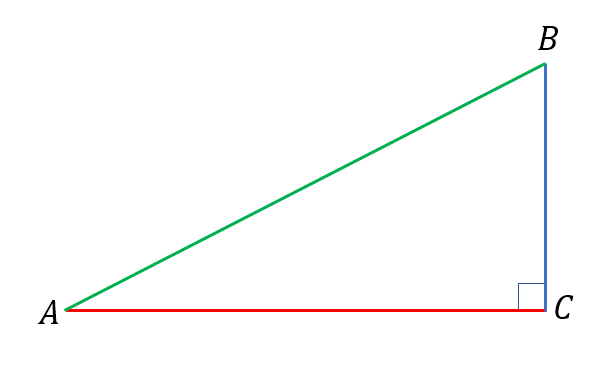
Сторона \(\color{green}{AB}\) знаходиться навпроти кута \(90^\circ\). Її ми будемо називати гіпотенузою даного трикутника.
- Гіпотенузою прямокутного трикутника
- називають його сторону, протилежну до прямого кута.
Інші дві сторони \(\color{red}{AC}\) і \(\color{blue}{BC}\) є прилеглими до прямого кута. Їх будемо називати катетами цього трикутника.
- Катетами прямокутного трикутника
- називають його сторони, прилеглі до прямого кута.
Кути \(\angle A\) і \(\angle C\) — гострі. Таким чином, можемо сказати, що будь-який прямокутний трикутник має, крім прямого кута, два гострих кута, та сторони: гіпотенузу та два катети.
Властивості прямокутного трикутника
Тепер розглянемо деякі властивості прямокутного трикутника. Насправді, не всі вони є для нас абсолютно новими. Але їх доцільно узагальнити.
Насамперед, ми знаємо теорему про суму кутів трикутника. Із неї слідує, що
Приклад 1
У прямокутному \(\Delta SDF\, (\angle D=90^\circ)\) відомо, що \(\angle F=40^\circ\). Чому дорівнює \(\angle S\)?
Розв'язання:
За властивістю гострих кутів прямокутного трикутника \(\angle S + \angle F = 90^\circ\), звідки \(\angle S = 90^\circ - \angle F\), \(\angle S = 90^\circ - 40^\circ = 50^\circ\).
Відповідь: \(50^\circ\).
Гіпотенузу прямокутного трикутника можна розглядати як похилу, проведену до одного із катетів, а інший катет — як перпендикуляр до першого. Тому
У прямокутному трикутнику гіпотенуза більша за будь-який із його катетів.
Приклад 2
Чи може існувати прямокутний трикутник, катети якого дорівнюють \(3\,\text{дм}\) і \(5\,\text{дм}\), а гіпотенуза — \(4\,\text{дм}\)?
Розв'язання:
Гіпотенуза прямокутного трикутника більша за будь-який із його катетів, а в умові задачі \(4\,\text{дм} < 5\,\text{дм}\).
Відповідь: Ні.
Цікавою є властивість медіани прямокутного трикутника, проведеної із вершини прямого кута до його гіпотенузи:
У прямокутному трикутнику медіана, проведена до гіпотенузи, дорівнює половині гіпотенузи.
Приклад
3
Сторони прямокутного трикутника дорівнюють \(9\,\text{см},\; 15\,\text{см і } 12\,\text{см}\). Знайдіть довжину медіани, проведеної до гіпотенузи цього трикутника.
Розв'язання:
Гіпотенуза прямокутного трикутника більша за будь-який із його катетів, в умові задачі це \(15\,\text{см}\). Медіана, проведена до гіпотенузи, дорівнює її половині: \(\frac{15\,\text{см}}{2}=7{,}5\,\text{см}\).
Відповідь: \(7{,}5\,\text{см}\).
Із останньої властивості можна зробити важливий висновок:
Медіана, проведена до гіпотенузи прямокутного трикутника, ділить його на два рівнобедрених трикутники.
І, нарешті, остання властивість:
Якщо у прямокутному трикутнику один з гострих кутів дорівнює 30°, то протилежний цьому куту катет дорівнює половині гіпотенузи
Приклад
4
У прямокутному трикутнику \(KLM\;\left(\angle L=90^\circ\right)\) відомий \(\angle K = 60^\circ\) та сторона \(KM=18\,\text{см}\). Знайдіть сторону \(KL\).
Розв'язання:
Покажемо даний трикутник на малюнку:
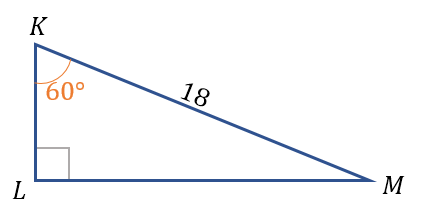
З малюнка бачимо, що відома сторона \(KM\) є гіпотенузою трикутника. Шуканий катет \(KL\) — протилежний до \(\angle M\). В свою чергу, \(\angle M=90^\circ - \angle K\). \(\angle M=90^\circ-60^\circ=30^\circ\). Тобто, катет \(KL\) знаходиться навпроти кута \(30^\circ\), тому він дорівнює половині гіпотенузи \(KM\).
\(KL=\frac{1}{2}KM\).
\(KL=\frac{1}{2}\cdot 18=9\,\text{см}\).
Відповідь: \(9\,\text{см}\).

У прямокутному трикутнику сума гострих кутів дорівнює \(90^\circ\).