Системи лінійних рівнянь з двома змінними. Графічний метод розв'язування систем
Системи лінійних рівнянь з двома змінними
Існують такі рівняння з двома змінними, які мають спільні розв'язки. Наприклад, пара чисел \((1;\,3)\) є одночасно розв'язком рівняння \(4x+3y=13\) і рівняння \(5y-6x=9\).
Якщо перед нами стоїть завдання знайти всі спільні розв'язки двох рівнянь, то говорять, що потрібно розв'язати систему рівнянь. На письмі рівняння у систему об'єднують за допомогою фігурної дужки зліва. Ось так: \[\begin{cases} 4x+3y=13,\\5y-6x=9.\end{cases}\]
Зверніть увагу: після першого рівняння ставимо кому.
В нашому випадку обидва рівняння, що утворюють систему, є лінійними рівняннями з двома змінними. Тому таку систему називають системою двох лінійних рівнянь з двома змінними.
- Розв'язком системи рівнянь з двома змінними
- називають пару значень змінних, яка перетворює кожне рівняння у правильну рівність.
Подібно до того, як ми говорили, що означає розв'язати рівняння з двома змінними, вкажемо, що означає розв'язати систему:
- Розв'язати систему рівнянь —
- означає вказати всі її розв'язки, або довести, що їх не існує.
Існує декілька методів розв'язування систем лінійних рівнянь з двома змінними. Тут ми познайомимося із одним із таких способів.
Графічний метод розв'язування систем
Щоб розібратися із тим. що таке графічний метод розв'язування систем рівнянь, знову звернемося до системи \[\begin{cases} 4x+3y=13,\\5y-6x=9.\end{cases}\]
Побудуємо в одній системі координат графіки обох рівнянь:
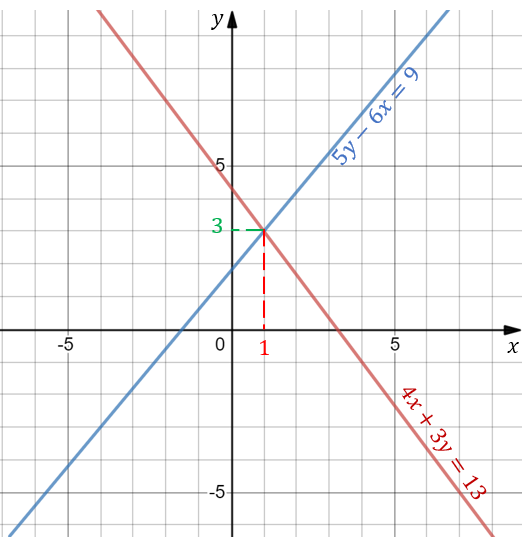
З малюнка видно, що дані графіки перетнулися в одній точці. Ця точка належить обом прямим одночасно, а, отже координати цієї точки \((\color{red}{1};\;\color{#00B050}{3})\) є розв'язком кожного із рівнянь. І ця точка єдина. Таким чином, ми розв'язали дану систему за допомогою графіків. Звідси і назва: графічний метод. При розв'язуванні подібних завдань зручно користуватися наступним алгоритмом:
Алгоритм розв'язування систем рівнянь графічним методом
- Побудувати на одній координатній площині графіки рівнянь, що входять до системи
- Знайти координати всіх точок перетину графіків
- Записати отримані пари чисел у відповідь
Якщо отримані графіки не перетинаються — система розв'язків не має.
Розглянемо ще один приклад на розв'язування системи лінійних рівнянь з двома змінними графічним методом.
Приклад 1 (приклад 4 із №1010 підручника)
Розв'яжіть графічно систему рівнянь: \[\begin{cases}2x+3y=6,\\3x-y=9.\end{cases}\]
Розв'язання:
Побудуємо на одній координатній площині графіки обох рівнянь:
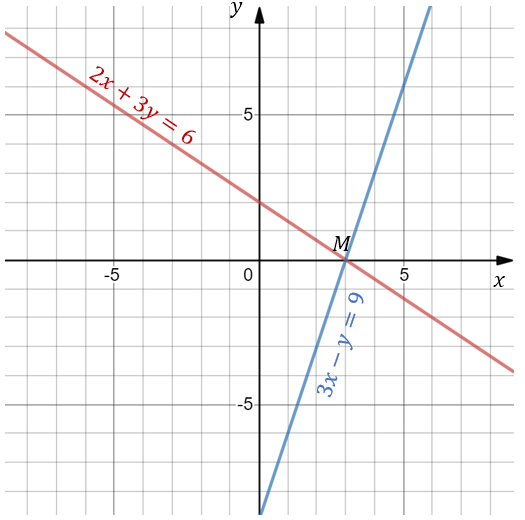
З малюнка визначаємо, що отримані графіки перетнулися в одній точці \(M(3;\,0)\). Координати цієї точки і є розв'язком системи.
Відповідь: \((3;\,0)\).

Декілька рівнянь, об'єднані фігурною дужкою, називаються системою рівнянь.