3. Область значень функції
3.1 Що таке область значень функції
Якщо для змінної \(x\) існує область визначення функції, то мусить існувати своя область і для змінної \(y.\)
Така область дійсно існує. В неї об'єднані всі значення, яких може набувати ця змінна, і називається вона областю значень функції.
- Областю значень функції
- називають сукупність усіх значень, яких може набувати функція.
Область значень функції позначають \(E(y)\).
Нагадаємо, які області значень мають функції, розглянуті у сьомому та восьмому класах:
3.2 Область значень лінійної функції \(y=kx+b\)
При \(k\ne0\)
Як видно із графіка функції \(y=6x+2\), при значеннях коефіцієнта \(k\neq0\), область значень лінійної функції — всі дійсні числа. Або можна вказати це саме проміжком: \(E(y)=(-\infty;{ }+\infty).\)
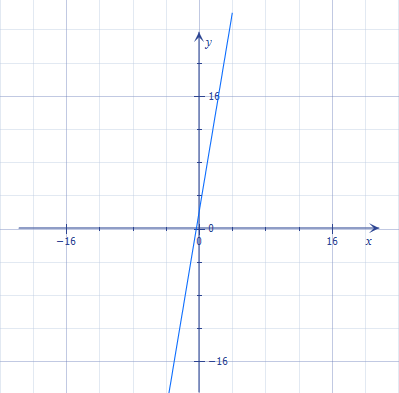
При \(k=0\)
Якщо коефіцієнт \(k=0\), то функція набуває вигляду \(y=b\), і, область її значень, відповідно, \(E(y)=b.\) На малюнку показано графік функції \(y=3\), який гарно це ілюструє.

З малюнка видно, що за будь-яких значень \(x\) функція набуває значення \(3,\) тобто \(E(y)=3.\) Такі функції ще називаються сталими функціями, або константами.
3.3 Область значень функції \(y=\frac{k}{x}\)
Функція \(y=\frac{k}{x},\) яку ще називають оберненою пропорційністю, має собі за графіка криву лінію, яку називають гіпербола. Ця крива нескінченно наближається до осі \(Oy\), не дотикаючись до неї, і не перетинаючи її. Звідси легко зробити висновок, що областю значень даної функції є всі числа, окрім нуля.
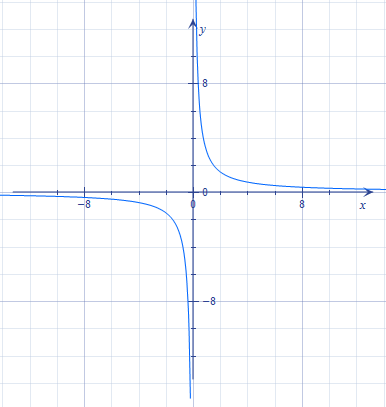
Проміжком це запишеться \(E(y)=(-\infty;\text{ } 0)\cup(0;{ }+\infty).\) На малюнку зображено графік функції \(y=\frac{1}{x}\). Якщо число \(k\) буде від'ємним, то графік потрібно "відзеркалити" відносно осі \(Oy\). Область визначення функції при цьому не зміниться.
3.4 Область значень функції \(y=x^2\)
Графіком цієї функції є парабола. Вершина параболи знаходиться у точці \(O(0;\text{ }0)\), а вітки прямують вгору.
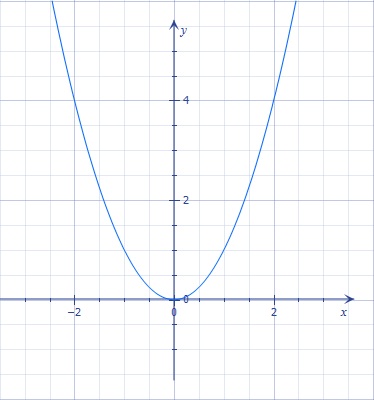
Область значень функції \(y=x^2\) можна записати \(E(y)=[0;{ }+\infty).\)
3.5 Область значень функції \(y=\sqrt{x}\)
Нагадаємо графік функції \(y=\sqrt{x}.\)
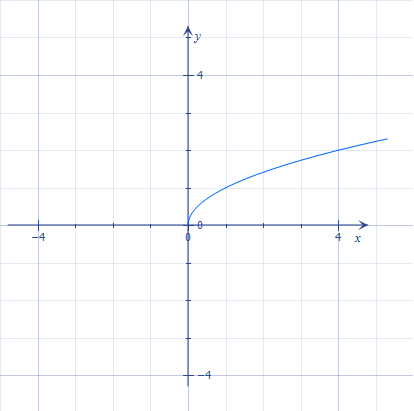
З цього графіка видно, що координати \(y\) точок на ньому набувають лише невід'ємних значень. Отже, область значень даної функції: \(E(y)=[0;\text{ }+\infty)\).
Далі в цьому курсі ми ознайомимося, як знаходити область значень квадратичної функції.
< Попередня тема Наступна тема >
