5. Проміжки знакосталості функції
5.1 Що таке проміжки знакосталості. Означення
Легко помітити, що на Мал.1 нулі функції розбили область визначення на окремі проміжки. Ці проміжки є проміжками знакосталості функції. На кожному із них функція не змінює свого знаку. Вона або строго додатна, або строго від'ємна.
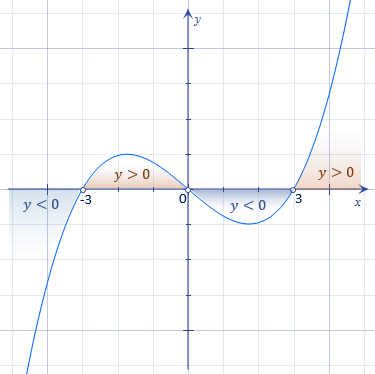
- Проміжками знакосталості функції
- називають проміжки області визначення, на яких функція зберігає свій знак (тобто залишається додатною або від'ємною)
Знайти проміжки знакосталості функції означає вказати самі ці проміжки, а також знак функції на кожному з них. Таке завдання можна, так само, виконувати двома способами: аналітично і за графіком функції.
5.2 Як знаходити проміжки знакосталості функції, заданої формулою
Якщо функцію задано аналітично (тобто формулою), то проміжки знакосталості зручно знаходити методом інтервалів. Для цього слід скористатися наступним алгоритмом:
Подивимось, як виконувати такі завдання.
Приклад:
Знайдіть проміжки знакосталості функції
\(y=\frac{3x-6}{\sqrt{4+x}}\)
Розв'язання:
1. Знайдемо область визначення функції:
\(4+x>0,\)
\(x>-4;\)
\(D(y)=(-4;\text{ } +\infty).\)
2. Знайдемо нулі функції з умови \(y=0:\)
\(\frac{3x-6}{\sqrt{4+x}}=0,\)
\(3x-6=0,\)
\(x=2.\)
Маємо
\(y=0 \text{ при } x=2.\)
3. Покажемо на числовій прямій проміжки, на які точка \(x=2\) розбиває область визначення:
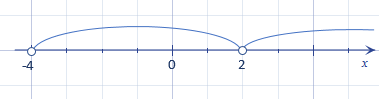
Це і є проміжки знакосталості нашої функції: \((-4;\text{ } 2)\) і \((2; \text{ }+\infty).\)
4. Тепер визначимо, якого ж знаку набуває функція на кожному з цих проміжків.
З першого проміжку \((-4;\text{ }2)\) візьмемо довільне значення (наприклад \(0\)) і підставимо замість \(x\) у рівняння функції:
\[y(0)=\frac{3 \cdot 0 - 6}{\sqrt{4+0}}=-\frac{6}{2}=-1{,}5.\]
Маємо, що \(y(0)<0,\) тобто наша функція на проміжку \((-4; \text{ } 2)\) набуває від'ємних значень.
На другому проміжку візьмемо \(x=5\). Будемо мати: \[ y(5) = \frac{3 \cdot 5 -6}{\sqrt{4+5}}=\frac{9}{\sqrt{9}}=3.\]
Отримали додатне значення. Це означає, що функція додатна на проміжку \((2; \text{ }+\infty)\).
Проілюструємо це на малюнку (поставимо відповідні знаки над кожним проміжком):
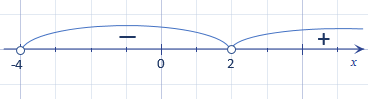
5. Все, що залишилося — записати відповідь.
Відповідь:
\(y<0: \text{ }(-4; \text{ } 2),\)
\(y>0: \text{ }(2; \text{ }+\infty).\)
Ось так визначають проміжки знакосталості функції методом інтервалів. В багатьох випадках набагато зручніше знаходити ці проміжки, використовуючи графік функції.
5.3 Як знаходити проміжки знакосталості функції за її графіком
Якщо функцію задано її графіком, або цей графік легко побудувати, то проміжки знакосталості знаходимо так:
Як шукати проміжки знакосталості за графіком функції
- На осі іксів ми вже маємо і область визначення, і нулі функції. Ними вісь поділена на проміжки знакосталості.
- Якщо на проміжку графік функції розміщений нижче осі іксів, то функція від'ємна.
- Якщо на проміжку знакосталості графік розміщений вище осі іксів, то функція додатна.
- Записати відпвідь
Спробуємо використати цю схему до функції із попереднього прикладу, але вже з побудованим графіком в умові задачі.
Приклад:
Знайти проміжки знакосталості функції \(y=\frac{3x-6}{\sqrt{4+x}}\) за її графіком (Мал. 4).
Розв'язання:
Роздивимось уважно графік даної функції. З нього видно, що область визначення \(D(y)=(-4; \text{ }+\infty).\)
Графік перетинає вісь \(Ox\) в точці \(2\) (нуль функції). Ця точка розбила область визначення на проміжки \((-4; \text{ } 2)\) і \((2; \text{ } +\infty).\)
На першому із вказаних проміжків графік проходить нижче осі абсцис ("іксів"). На Мал. 5 це показано блакитним. Тут функція має знак "мінус".
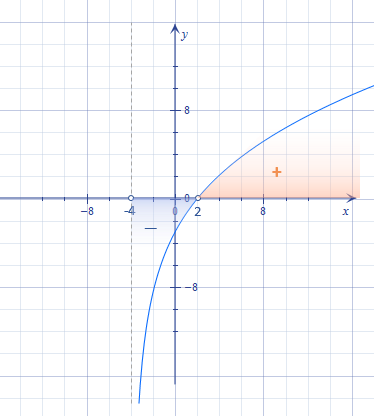
На проміжку \((2; \text{ }+\infty)\) графік знаходиться вище осі \(Ox\) (показано рожевим). Функція, відповідно, має знак "плюс".
Відповідь:
\(y<0: \text{ }(-4; \text{ } 2),\)
\(y>0: \text{ }(2; \text{ }+\infty).\)
< Попередня тема Наступна тема >

Метод інтервалів для знаходження проміжків знакосталості функції: