4. Нулі функції
4.1 Нулі функції. Означення
З нулями функції все досить просто. Це такі значення \(x\), при яких отримуємо, що \(y=0.\)
- Нулями функції
- називають значення аргументу, при яких функція набуває значення нуль.
Нулі функції знаходити досить легко як за формулою, що задає функцію, так і за графіком цієї функції.
4.2 Як знаходити нулі функції за її формулою
У математиці функцію найчастіше задають аналітично. Тому необхідно уміти розв'язувати завдання на знаходження нулів функції за її формулою.
Логіка тут просто-таки залізна. Якщо ліва частина рівняння дорівнює нулю, то і права теж дорівнює нулю. Між ними стоїть же знак дорівнює! Якщо маємо функцію \(y=f(x),\) і \(y=0\) (бо ж таки нулі функції), то і \(f(x)=0.\)
Приклад 1:
Знайти нулі функції \(y=3x-5.\)
Розв'язання:
Записуємо \(3x-5=0\) і розв'язуємо це рівняння.
\(3x=5,\)
\(x=1\frac{2}{3}\)
Відповідь: \(1\frac{2}{3}\).
Приклад 2:
Знайти нулі функції \(y=x^3-9x.\)
Розв'язання:
Записуємо
\(x^3-9x=0\), винесемо \(x\) за дужки:
\(x(x^2-9)=0\), що рівносильно розв'язуванню сукупності рівнянь:
\( \left[ {\begin{array}{*{20}c} {x_1 = 0,} \hfill \\ {x^2 - 9 = 0;} \hfill \\ \end{array}} \right.\) \( \Rightarrow\) \(\left[ {\begin{array}{*{20}c} {x_{1} = 0,} \hfill \\ {x^2 = 9;} \hfill \\ \end{array}} \right. \) \( \Rightarrow\) \(\left[ {\begin{array}{*{20}c} {x_{1} = 0,} \hfill \\ {x = \sqrt{9};} \hfill \\ \end{array}} \right. \) \(\Rightarrow\) \(\left[ {\begin{array}{*{20}c} {x_{1} = 0,} \hfill \\ {x_2 = -3, \text{ } x_3=3.} \hfill \\ \end{array}} \right. \)
Дана сукупність має три корені, отже у нашої функції є аж три нулі.
Відповідь: \(-3; \text{ }0; \text{ }3 \)
Отже, якщо функцію задано формулою виду \(y=f(x)\), то, щоб знайти її нулі, достатньо розв'язати рівняння \(f(x)=0.\) Отримані корені і є нулями функції.
4.3 Як знаходити нулі функції за її графіком
Якщо функцію задано графічно, то її нулі знаходити ще легше. Про прямокутну систему координат ми знаємо, що координати \(y\) всіх точок на осі \(Ox\) дорівнюють нулю. Отже,
Щоб знайти нулі функції, заданої графіком, досить вказати координату \(x\) точок, в яких цей графік перетинає вісь \(Ox\).
Приклад:
Знайти нулі функції \(y=x^3-9x\) за її графіком.
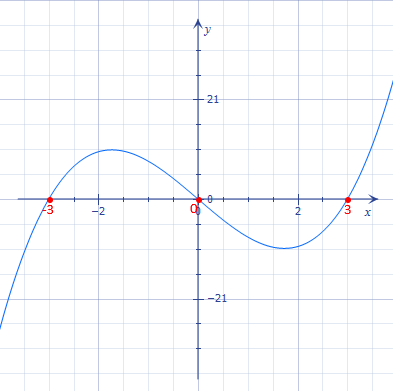
Розв'язання:
З Мал.1 видно, що графік функції перетинає вісь іксів у точках з координатами \(x,\) що дорівнюють \(-3, \text{ }0,\) і \(3.\)
Ці числа і є нулями даної функції.
Відповідь: \(-3; \text{ }0; \text{ }3. \)
Як і обіцяв, усе дуже просто.
< Попередня тема Наступна тема >

Щоб знайти нулі функції, заданої формулою, потрібно праву частину прирівняти до нуля і розв'язати отримане рівняння.