6. Проміжки зростання і спадання функції
6.1 Що таке проміжки зростання і що таке проміжки спадання функції
Про функцію говорять, що вона зростає, якщо для будь-яких двох значень аргументу справджується наступне: значення функції буде більшим для більшого значення аргументу, і меншим — для меншого.
Наприклад:
Зростаючою є функція \(y=3x+2\).
Візьмемо довільні два значення
аргументу, нехай \(x_1=-5\) і \(x_2=-2\). Для них матимемо:
\(y(x_1)=3\cdot(-5)+2=-13\) і \(y(x_2)=3\cdot(-2)+2=-4\). Тобто,
для \(x_2>x_1\) справджується, що \(y(x_2)>y(x_1)\)
Про функцію кажуть, що вона спадає, якщо навпаки, більшому значенню аргументу відповідає менше значення функції.
Наприклад:
Спадаючою є функція \(y=-3x+2\).
Візьмемо довільні два значення
аргументу, нехай \(x_1=-5\) і \(x_2=2\). Для них матимемо:
\(y(x_1)=-3\cdot(-5)+2=17\) і \(y(x_2)=-3\cdot2+2=-4\). Тобто,
для \(x_2>x_1\) справджується, що \(y(x_2)<y(x_1)\)
У розглянутих прикладах кожна із функцій зростала або спадала на всій області визначення. Наразі, існує багато функцій, які на окремих проміжках області визначення зростають, а на якихось інших проміжках - спадають. Це добре видно на прикладі функції \(y=x^2\). Дана функція спадає на проміжку \((-\infty; 0)\) і зростає на \((0; +\infty)\). Проілюструємо сказане не графіку:
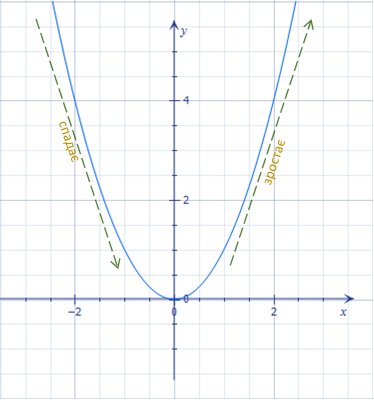
Як бачите, за графіком функції досить легко визначати її проміжки зростання та спадання. Для цього достатньо подивитися, від якого значення і до якого по осі \(Ox\) графік іде вгору (функція зростає), і між якими значеннями графік прямує вниз (функція спадає). Отриманні значення \(x\) слід записати як межі відповідних проміжків.
Враховуючи все сказане, можемо дати повне означення зростаючої та спадаючої функції на проміжку:
- Функція \(y=f(x)\) називається зростаючою на деякому проміжку,
- якщо для будь-яких \(x_1\) і \(x_2\), що належать цьому проміжку, із умови \(x_1>x_2\) слідує, що \(f(x_1)>f(x_2)\). Сам цей проміжок називається проміжком зростання функції
- Функція \(y=f(x)\) називається спадаючою на деякому проміжку,
- якщо для будь-яких \(x_1\) і \(x_2\), що належать цьому проміжку, із умови \(x_1>x_2\) слідує, що \(f(x_1)<f(x_2)\). Сам цей проміжок називається проміжком спадання функції
Проміжки зростання і спадання функції можна знаходити й аналітично. Але для цього використовується похідна функції, з якою ви познайомитесь в курсі 10-11 класу.
< Попередня тема Наступна тема >
