Лінійні рівняння з двома змінними
Рівняння з двома змінними
На практиці доводиться мати справу із ситуаціями, коли невідомими є дві величини одночасно.
Розглянемо такий випадок: на будівництво якогось об'єкту потрібно завезти цемент для мулярів та фарбу для малярів. Цемент фасується у мішки по \(50\,\text{кг}\), а фарба — у банки по \(10\,\text{кг}\). При цьому автомобіль, який прямує до об'єкту, може взяти не більше \(2\,\text{т}\) вантажу. Скільки мішків цементу та банок фарби вантажити?
Розв'язуючи цю задачу, можна скласти рівняння: \[50\color{#008000}{x}+10\color{#1e90ff}{y}=2000,\] де \(\color{#008000}{x}\) — кількість мішків цементу, а \(\color{#1e90ff}y\) — кількість банок фарби. Маємо одне рівняння з двома змінними.
Які числа є розв'язком цього рівняння? Давайте подивимось. Якщо цементу візьмуть \(30\) мішків \(\left(\color{#008000}{x=30}\right)\), то фарби можна взяти \(50\) банок \(\left(\color{#1e90ff}{y=50}\right)\). Дійсно, \[50\cdot\color{#008000}{30}+10\cdot\color{#1E90FF}{50}=2000\,.\]
Отже, розв'язком цього рівняння є пара чисел \(\color{#008000}{x=30}\,,\;\color{#1e90ff}{y=50}\). Це записують так: \(\left(30;\,50\right)\).
Зрозуміло, що це не єдиний варіант того, як можна завантажити автомобіль цементом та фарбою. Можна взяти \(32\) мішки цементу та \(40\) банок фарби, і пара чисел \(\left(32;\,40\right)\) — теж розв'язок рівняння. І таких розв'язків є дуже багато. Головне, знати, що
- Розв'язком рівняння з двома змінними
- називають пару значень змінних, які перетворюють рівняння у правильну рівність.
Якщо розглядати рівняння \(50x+10y=2000\) не з умови задачі, а як просто рівняння, яке потрібно розв'язати, то воно має безліч розв'язків, серед яких будуть і від'ємні, і дробові числа. Таких рівнянь (із безліччю розв'язків) є дуже багато.
Важливо розуміти, що якщо пара \(\left(3;\,5\right)\) є розв'язком рівняння \(x+y=8\), і пара \(\left(5;\,3\right)\) є розв'язком цього ж рівняння, то це — два різних розв'язки.
Існують рівняння з двома змінними, які взагалі не мають жодного розв'язку. Наприклад, рівняння \(x^2+y^2=-3\) не має розв'язків.
Разом з тим, існують такі рівняння, які мають єдиний розв'язок. Таким чином
Вкажемо тепер, що означає розв'язати рівняння із двома змінними.
- Розв'язати рівняння з двома змінними —
- це означає знайти всі його розв'язки, або довести, що їх не існує.
При розв'язуванні рівнянь із двома змінними можна використовувати всі ті властивості рівнянь, якими користувалися, коли розв'язували рівняння із однією змінною.
Лінійне рівняння з двома змінними
Серед усіх видів рівнянь з двома змінними можна виділити лінійні рівняння. Дамо означення:
- Лінійним рівнянням з двома змінними
- називають рівняння виду
\[ax+by=c,\] де \(x\) і \(y\) — змінні, \(a,\,b,\,c\) — деякі числа.
Числа \(a,\,b,\,c\) мають такі назви:
- \(a\) — коефіцієнт при змінній \(x\);
- \(b\) — коефіцієнт при змінній \(y\);
- \(c\) — вільний член.
Приклади лінійних рівнянь з двома змінними:
\(x+y=15;\;\)
\(-3x+3{,}25y=-7;\;\)
\(7-3x=5y;\;\)
\(2+\frac{2}{3}x-4y=\frac{5}{7}.\)
Графік рівняння з двома змінними
Будь-яке рівняння із двома змінними можна подати у вигляді, коли одна змінна є функцією від іншої змінної.
Наприклад, рівняння \(2\color{#008000}{x}+\color{#1e90ff}{y}=8\) можна записати у вигляді \(\color{#1e90ff}{y}=8-2\color{#008000}{x}\). В розглянутому прикладі можемо говорити, що змінна \(\color{#1e90ff}{y}\) є значенням функції, а змінна \(\color{#008000}{x}\) — її аргументом.
Ми знаємо, що всі пари чисел \(\left(\color{#008000}{x};\,\color{#1e90ff}{y}\right)\), де \(\color{#008000}{x}\) — аргумент функції, а \(\color{#1e90ff}{y}\) — відповідні їм значення, позначаються на координатній площині точками, які утворюють графік функції. Отже, є сенс говорити про графік рівняння з двома змінними:
- Графіком рівняння з двома змінними
- називають геометричну фігуру, що складається з усіх тих і тільки тих точок координатної площини, координати яких (пари чисел) є розв'язками даного рівняння.
Графік розглянутого рівняння \(2x+y=8\) представлений на Мал.1.
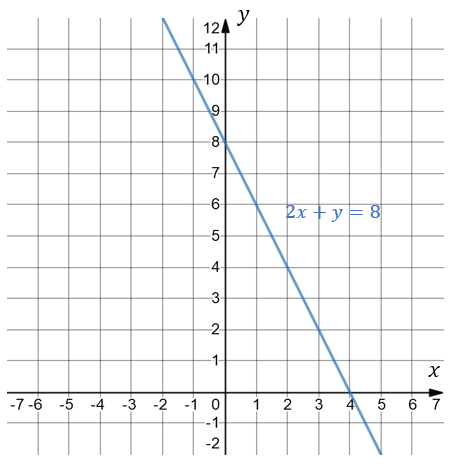
Неважко зробити висновок, що
Графіком лінійного рівняння з двома змінними є пряма.
Процес побудови графіка рівняння з двома змінними майже нічим не відрізняється від побудови графіка функції.
Приклади розв'язування завдань
Розглянемо декілька прикладів типових завдань із даної теми та їх розв'язування.
Приклад 1
Чи є пара чисел \(\left(-2;\,3\right)\) розв'язком рівняння \(4x+3y=1\)?
Розв'язання:
Щоб перевірити, чи пара чисел \(\left(-2;\,3\right)\) є розв'язком даного рівняння, підкладемо у нього значення змінних \(x=-2\) та \(y=3\):
\(4\cdot\left(-2\right)+3\cdot3=1,\)
\(-8+9=1,\)
\(1=1.\)
Отримали правильну рівність, отже пара чисел \(\left(-2;\,3\right)\) є розв'язком рівняння \(4x+3y=1\).
Відповідь: Так.
Приклад 2
Яка з пар чисел є розв'язком рівняння \(5x+3y=-6\)?
A) \(\left(6;\, 8\right)\);
B) \(\left(6;\, -8\right)\);
C) \(\left(3;\, -3\right)\);
D) \(\left(-3;\, 3\right)\).
Розв'язання:
Підставимо у дане рівняння замість \(x\) перше число кожної пари, а замість \(y\) — друге число цієї ж пари, та порівняємо результат дій у лівій частині рівняння із правою частиною :
A) \(5\cdot 6 +3\cdot 8 = 54 \ne -6\) — не задовільняє;
B) \(5\cdot 6 +3\cdot (-8) = -6 = -6\) — задовільняє;
C) \(5\cdot 3+3\cdot (-3) =6 \ne -6\) — не задовільняє;
D) \(5\cdot (-3) +3\cdot 3 = -6 = -6\) — задовільняє.
Дане рівняння задовільняють дві пари чисел — \(\left(6;\, -8\right)\) (варіант відповіді B)) та \(\left(-3;\, 3\right)\) (варіант відповіді D)).
Відповідь: B), D).
Приклад 3
Укажіть якийсь один розв'язок рівняння \(x+4y=1\)
Розв'язання:
Візьмемо будь-яке число замість змінної \(x\). Наприклад, \(x=2\). Підставимо це значення у рівняння:
\(2+4y=1\). Отримали рівняння з однією змінною \(y\). Розв'яжемо його:
\(4y=1-2,\)
\(4y=-1,\)
\(y=-1:4,\)
\(y=-0{,}25.\)
Отже, маємо пару чисел \(\left(2;\,-0{,}25\right)\), що є розв'язком даного рівняння.
Відповідь: \(\left(2;\,-0{,}25\right)\)
Приклад 4
Чи належить графіку рівняння \(2x^2-y+1=0\) точка \((2;\,9)\)?
Розв'язання:
Якщо точка належить графіку рівняння з двома змінними, то її координати перетворюють це рівняння у правильну рівність. Підставимо у наше рівняння значення змінних \(x=2\) та \(y=9\):
\(2\cdot 2^2-9+1=0,\)
\(8-9+1=0,\)
\(0=0.\)
Отримали правильну рівність, отже точка \((2;\,9)\) належить графіку рівняння \(2x^2-y+1=0\).
Відповідь: належить.
Приклад 5
Графік рівняння \(7x-5y=47\) проходить через точку \((6;\,b)\). Чому дорівнює значення \(b\)?
Розв'язання:
Підставивши координати точки до рівняння отримуємо:
\(7\cdot 6 -5b=47\). З отриманого рівняння знаходимо значення \(b\):
\(42-5b=47,\)
\(-5b=47-42,\)
\(-5b=5,\)
\(b=-1.\)
Відповідь: \(-1\).

Рівняння з двома змінними може: